
In the Beginning
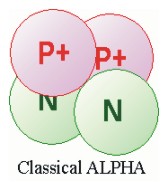
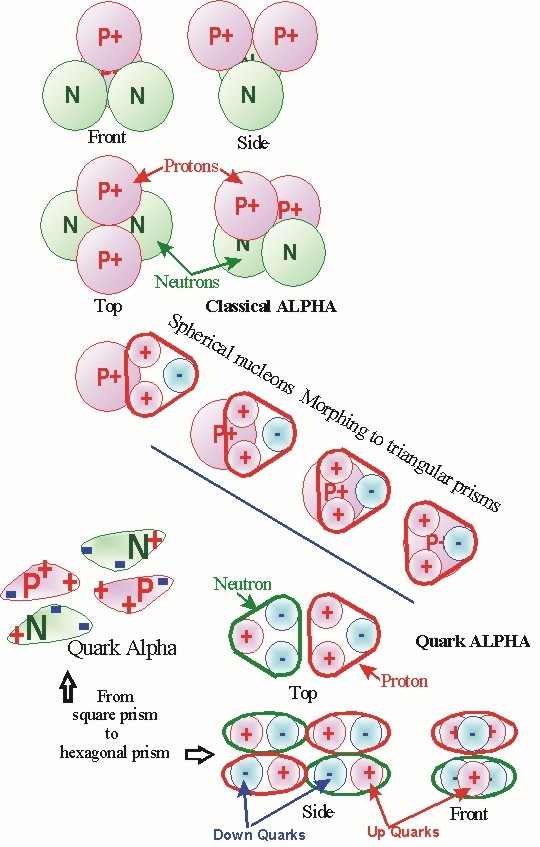
In this section we will compare the tetrahedral classical alpha particle predicted by the Standard Model
with the
proposed quark alpha particle predicted by the Hexagonal Lattice Model described in this paper.

The break through concepts around which this model is built, developed while studying shape and configuration of the alpha particle. The classical alpha predicted by the Standard Model is represented as a tetrahedron with the protons and neutron positioned at the vertices. In the classical model alpha configuration all the nucleons are nearest neighbors, which places the two protons next to each other.
However, nucleons are made up of three quarks, and quarks carry two types of charge, a color charge and an electrical charge. The �up� quark has a +2/3e charge and the �down� quark has a -1/3e charge. These are know fact, but has this knowledge been fully implemented into the Standard Nuclear Model? NO!
=================
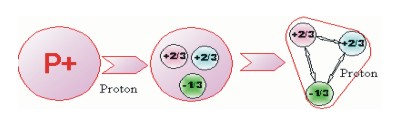
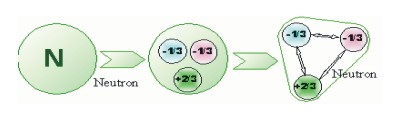
Our first break through came when we realized that three particles form a triangle not a sphere.
Our second break through came when it became obvious that the electrical charges of the quarks would line up for maximum coupling.
As shown in the previous section electric charges of the quarks can align the positive electrical charge with the negative electrical charge which will maximize the electrical coupling between the quarks in adjacent nucleons.
The exclusion principle holds quarks and other nucleons apart. The strong or color force pulls and holds everything together. Neither the color force nor the exclusion principle provide any torque or alignment force that could impose any type of structure on the nucleus. However, electric and magnetic forces always align in a preferential orientation. It is this preferential orientation or alignment of the electric and magnetic fields that controls the nuclear structure.
Electrons form shells because of the strong central positive force of the nucleus. But there is no known force concentrated at the center of the nucleus for proton to form shells around and then there are the neutrons that are neutral, what is the central force around which neutrons could form shells, and if there is some unknown central force, why are their separate shell structures for protons and neutrons? These facts like so many others are just glossed over in most books. Various anomalies that are not answered by current models are simply swept under the rug or ignored.
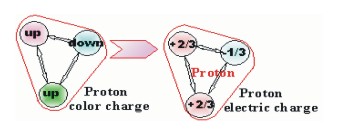
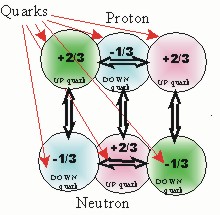
In subsequent illustrations, the color of quarks in illustrations will represent the electrical charge of the quark rather than the color charge,
red for positive 2/3 electrical charge
and
blue for negative 1/3 electrical charge.
Why separate by electrical charge?
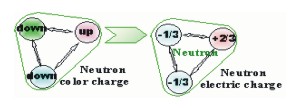
First, all quarks have color charge which is always present and is always attractive. The color force holds the nucleus together without preference to orientation. Because the color force is always the same and is always shifting from quark to quark but the color force does not control position or arrangement, labeling of color gluons will be obviated to simplify the presentation of this model
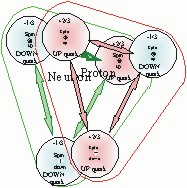
Second, The electric charges of the quarks are what differentiates the locations of the protons and neutrons in the nucleus. The up quarks have a + 2/3 charge and the down quarks have a - 1/3 charge. The only position where up quarks are nearest neighbors are in protons and the only place down quarks are nearest neighbors are in neutrons. Everywhere else in the nucleus nearest neighbors of an up quark are always a down quark. The important results is that protons are never nearest neighbors and neutrons are never nearest neighbors, protons and neutrons are always nearest neighbors. This is illustrated in the deuteron and the alpha particle models shown. The alignment of up and down quarks insures that protons are never nearest neighbors to other protons and neutrons are never nearest neighbors to other neutrons in the nucleus.
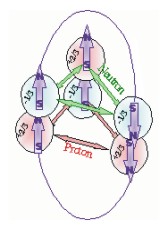
Third, all quarks have magnetic dipole that will align with adjacent magnetic dipoles. Magnetic field obey the law of superposition and thus there are micro and macro magnetic fields in the nucleus. The macro magnetic field defines the dipole moment of the nucleus. Superposition of the individual quark dipoles create the micro magnetic field that also controls and adjust the individual magnetic dipoles of the individual quarks. As all quarks have both a north pole and a south pole, which can create torque it is the magnetic field that will affect relative alignment and only slightly effect the relative position within the nucleus. It is the electric field of the quarks that controls the positions of the nucleons in the nucleus. As shown in the illustration the two down quarks in the neutron are oriented so their magnetic fields form a loop so they become part of the slightly larger magnetic loop. The two up quarks in the proton are oriented to also join each other to join in forming this slightly larger magnetic loop. A magnetic loop illustrated by the purple oval loop between up and down quarks illustrates the type of align that will maximize magnetic coupling. Even so the extra up quark in the neutron and the extra down quark in the proton align to give the deuteron a residual magnetic dipole. Because the magnetic fields are involved primarily in torque and not position in the nucleus, most of the following illustrations we will not display the magnetic fields. This sacrifice is for simplicity, however remember that the magnetic fields will also have an effect because of those dipoles which can add or subtract from the total forces binding the nucleus. It will be illustrated later in this paper how variations in the magnetic field in nuclei with odd "A" numbers help define how the nucleus is compensating for balance variations.
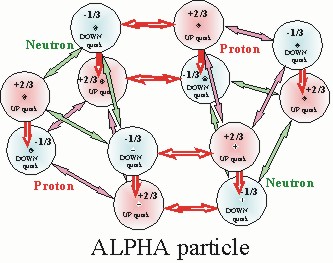
Quick Review
Rather than the old view of nucleons as spheres nucleons are in fact triangular particles with the three electrical charge quarks forming the corners.
Forces on the protons and neutron in the nucleus are more than just the strong force. The forces and their importance are summarized.
- 1. The Exclusion Principle keeps the nucleus from collapse
effect repulsive - 2. The strong force holds the protons and neutrons in the nucleus
effect attractive - 3. The color gluon force holds the quarks in the protons and neutrons.
effect attractive - 4. The electrical force aligns the protons and neutrons via their constituent quarks
effect attractive and repulsive - 5. The magnetic dipoles provides torque to help maintain balance in the nucleus
effect attractive, repulsive and torque
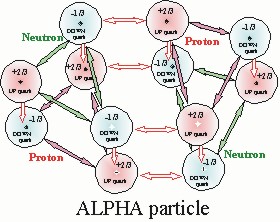
Nuclear rotation equates to a necessity for balance.
There are two types of balance in the nucleus.
The first and most important is centrally
radial balance measured with respect to
the center of mass of the nucleus.
The second is radial balance measured
from the central axis of the core.
- 6. Balance is the ultimate referee of nuclear stability
effect repulsive and torque
The figure of this alpha particle represent the general form that is used in this paper.
The following poster like figure summarizes how to view the shift in concept between the classic alpha particle predicted in the standard model and the quark alpha particle predicted by the hexagonal lattice model.
The data and information depicted in and on this web site are covered by © “copyright”.
The data and/or information presented in this web site may be used in part or whole if the user gives credit to the authors and references this web site.